FWHMの重要性について（なぜFWHMを求めるのか）２
Microsoft Excelを用いたコンピュータ・シュミレーション

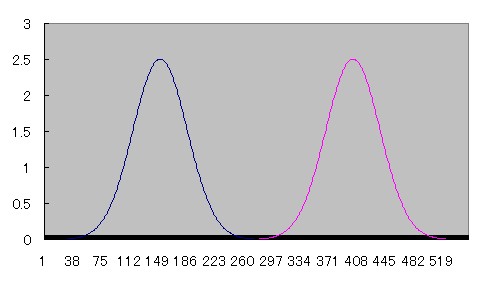
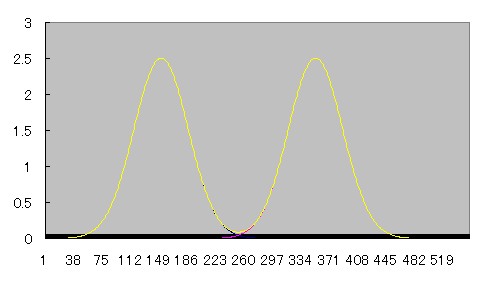
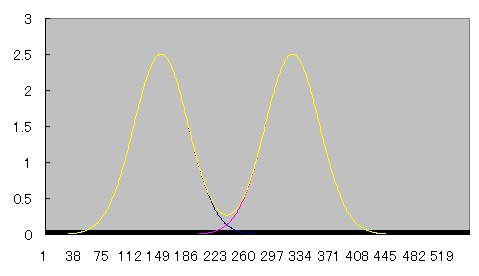
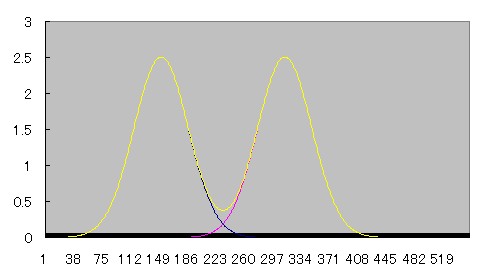
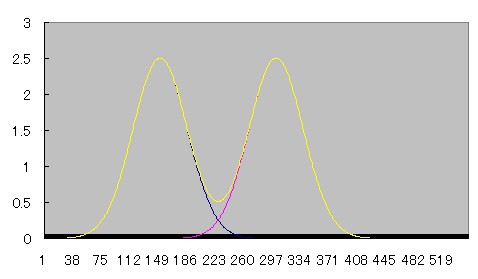
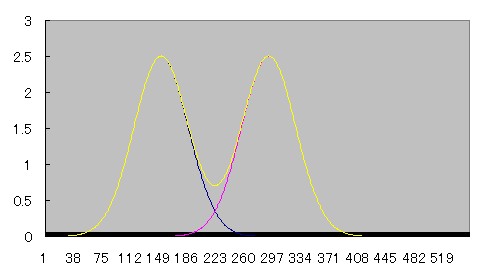
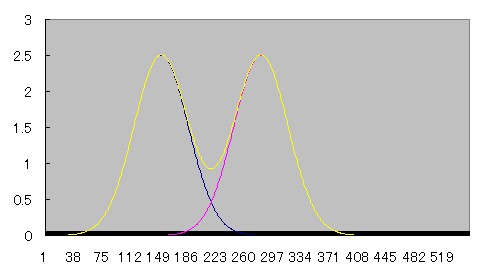
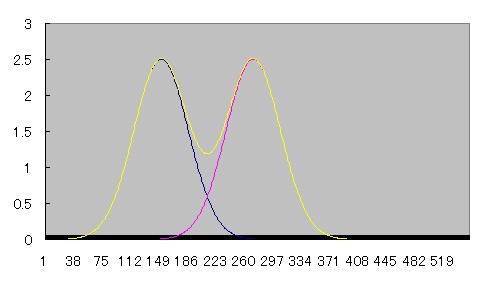
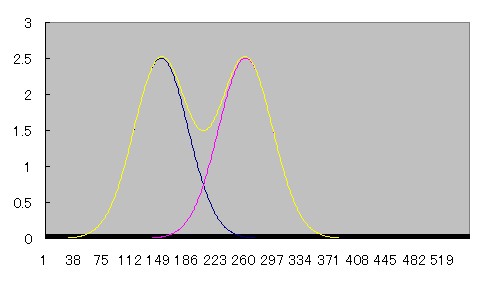
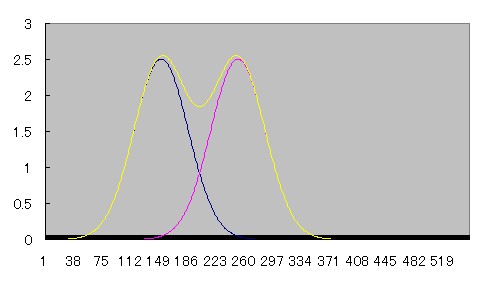
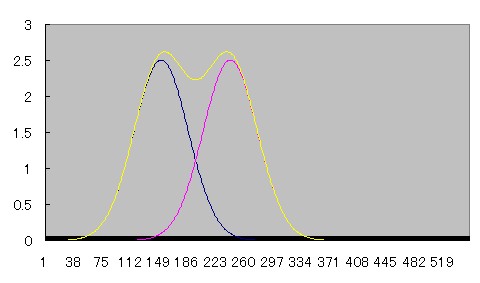
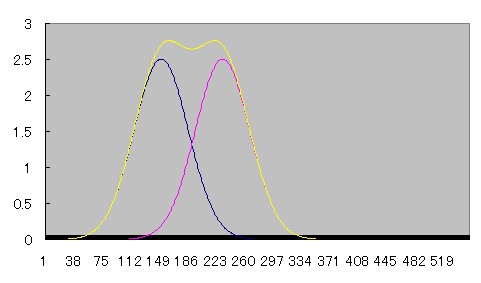
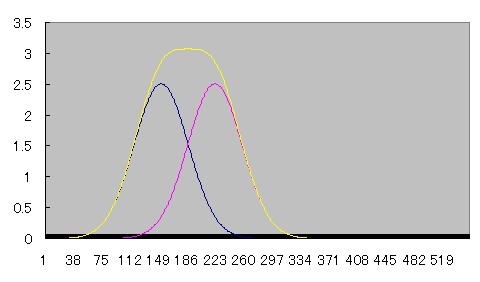
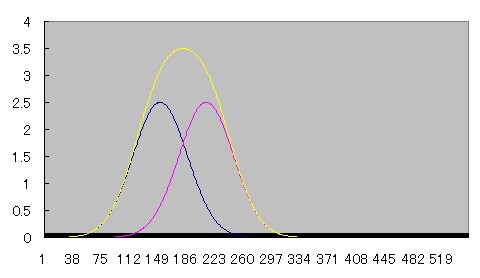
　２つの線源が近づいていくとprofile curveがどう重なり合っていくのか、Microsoft Excelを用いてシュミレーションしてみた。
　青とピンクのcurveは正規分布、黄色のcurveはその２つを加算したものである。



なかなかおもしろいでしょ？
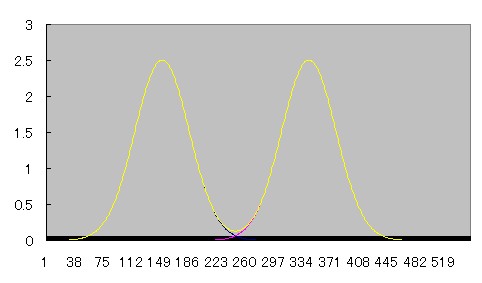
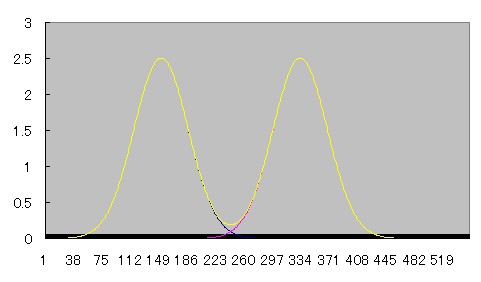
近づくにつれて徐々にふたつの間の谷間が浅くなり、やがて無くなる様子がわかる。
部分容積効果が起こって、ピーク値が上昇していることにも注目されたい。


　
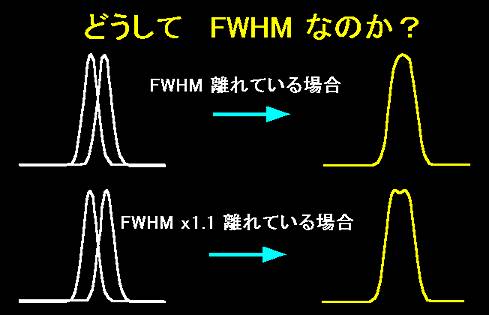
FWHMは「半値幅」である。ピークの半分の値になるときのcurveの幅である。
ふたつのcurveがFWHMの幅に近づくとき、curveの交点の値はピークの半分である。
ピークの半分の値が重なり合うわけだから、
ピークの半分の値　＋　ピークの半分の値　＝　ピーク値
したがって、このとき重なり合ったcurveはもとのcurveのピーク値になる。
ここがふたつの線源を分解する限界となる。
だから分解能の指標にFWHMを用いるのである。

注：実際には部分容積効果が起こってピーク値は上昇しているので、
　　FWHMの幅近づいたときには谷間がまだあり、
　　谷間がなくなるのは、もう少し近づいたときである。
　　「FWHMの重要性について（なぜFWHMを求めるのか）」の実験で、
　　線線源を5mmの中心間距離で並べたのにFWHMが5.66mmのときまで分解できたのも、
　　同じ理由ではないかと思われる。


技術情報・基礎編に戻る

メインに戻る

千葉核技研トップページへ

(c)Copyright 2002,The CHIBA Society of Nuclear Medicine Technology